Affect-Relations: Structural
Structural affect-relations are the configuration of connectedness of components.
Note:
- Structural affect-relations typically endure for some period of existence within a system. For example, in the human nervous system, neurons are interconnected in a unique configuration for each person. Structures can change, reflected by changes in configuration from time 1 to time 2. See below discussion of structural property values.
- Structural affect-relations are different from those for temporal affect-relations.
- This term is pronounced: STRUC-tu-ral af-FECT re-LA-tions, with emphases on the capitalized syllables.
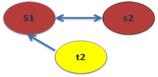
For example, in the image to the right, the 'guides the learning of' affect-relation is depicted. ‘Affect-relation’ is used in the sense of a verb—e.g., x affects y. The affect-relation set for the 'guides the learning of' relation: P('guides the learning of') = {(S1,s2), (s2,S1), (t2,S1)} is another way of characterizing what is illustrated in the digraph (directed graph) in the image.
During the observation of this small system, S1 'guides the learning of' s2; s2 'guides the learning of' S1; and t2 'guides the learning of' S1. This configuration persists over some period of time (e.g., 9 months) and represents system structure for the 'guides the learning of' affect-relation. S1, s2, and t2 are specific components of the system. In this case the components are specific persons: e.g., S1 is Susie, s2 is Samatha, and t2 is Todd.
An example of multiple affect-relation sets is illustrated by contrasting structural maps in the below image, one for Classroom X, and one for Classroom Y.

Assume that Goals 1 to 5 are important goals for students to achieve that prepare them for careers in science, technology, engineering and mathematics (STEM). For example, each goal could be a state standard for STEM learning achievement.
Each goal is a content component. Furthermore, notice that these goals are not independent but instead related to each other. For example, Goal 2 is a prerequisite to Goals 3, 4 and 5. Thus, the dashed lines with arrows represent the 'prerequisite to' affect-relation set. Notice also that the curriculum goal maps for Classroom X and Y are identical, as can be seen in the gray shaded areas in the top part of the above image. Both classrooms are trying to help students achieve the same STEM goals/standards.
Instructional units are also content components, represented by uppercase letters, A-I in the two maps. An instructional unit might be a group of classroom activities over a one-week period that a teacher has designed and implemented (i.e., lesson plans). These instructional units are connected to the goal components, depicted by the solid lines. The affect-relation set here might be named, "aims to achieve". For example, instructional unit A in Classroom X 'aims to achieve' both Goal 1 and Goal 2.
Students in each classroom are further components, labeled by circles 1-30 in Classroom X, and likewise in Y for a different group of 30 students. A solid line indicates that a specific student has mastered the learning objectives in the instructional unit ('mastery of' affect-relation), whereas a dashed line indicates the 'partial mastery of' affect-relation. No line between a student and an instructional unit means that the student failed to master objectives of that unit.
The overall connectedness in the two classrooms is quite different. Classroom X is more strongly connected than is Y, even though they have identical curriculum goal structures. In the map of Classroom X, more students have mastered objectives in the instructional units, and those units in turn are more connected to the curriculum goal structure—when compared with Classroom Y’s map.
The maps above go beyond what typical curriculum maps represent. Notice that these maps also include instructional units (IUs) that each classroom has completed over a period of 3 months, and the linkages of those IUs to each curriculum goal. For example in Classroom X, note that Goal 1 is supported by IUs A and B, and that Goal 2 is supported by IUs A, B, C and D. Alternatively, in Classroom Y, Goal 1 is not supported by any instructional unit, and Goal 2 is supported by H only. Finally, note how students in each classroom are connected to each instructional unit.
The "dashboards" below each map above have guages which indicate measures of structural properties of each map, such as: strongness, flexibleness, wholeness, etc. Axiomatic Theories of Intentional Systems defines these properties and provides measures of property values. For example, strongness has a value of 70 in Classroom X, whereas in Classroom Y strongness is 50. Strongness is characterized by affect-relations that are the directed-connected shortest-path-length between any two components.
